第２．２　捨てる、削る、順位をつける

１００％を求めなければバッサリと削れる　（2.2.1）

 

情報の選別をしようと思ったら、１００％を求めないということが、とても重要です。

 

例えば、先に見た「２対８」の法則。問題の８割は２割の範囲から出ている。そこで、もし１００％を求めず、８０パーセントでいいと満足するなら、２０％の範囲にだけ勉強を集中し、８０％の範囲には手を付けない、という思い切った選別ができるわけです。ところが、もし１００％のことを考えるならば、残りの２０％を埋めるために、あと８０％分の勉強をしなければならなくなります。しかしそうすると、結局「敵」は小さくなりません。ですから、ここは、バッサリと２０％を切り捨てて、８０％の出題にかけてみることにする。そうすると、勉強すべき範囲は従来の２０％にまで縮小します。

 

これが「敵を小さくする」という戦略です。

 

実は、この戦略に関する逸話が、岩波文庫の中にある金谷治訳注『新版孫子』の中の末尾の付録「孫子伝」の中に出てきます。孫ひんが、自分を救ってくれた田忌のために、賭け事へのアドバイスをするシーンです。こういう話です。

 

賭け事は、敵方と身方側とで、３頭ずつの馬を出し、３回の競走させることで行われてしました。そして、それぞれのもつ３頭の馬には、それぞれ上等・中等・下等の馬がおり、それぞれの速さが同等くらいでなので、競走はいつも勝ったり負けたりでした。このような状況の中で、孫ひんは、自己の主君・田忌に対して、大きく賭けることを勧めると共に、次のようにアドバイスしました。

 

 

そして、田忌がこのとおりにすると、田忌は、１度は負けたものの、２度の勝利を収め、結果的に大きく儲けることができた、という話です。

 

 

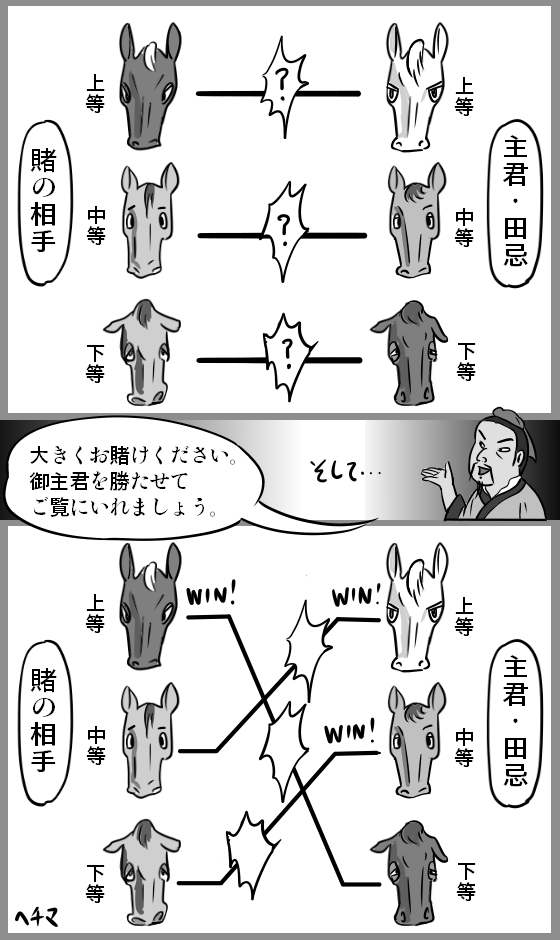
この話は、あまりに出来過ぎているので、フィクションではないかと言われているそうですが、敵を小さくする好例であることは間違いありません。つまり、あえて１つの競走を捨てることで、あとの２つの競走での勝利を確実なものとする、という考え方です。つまり、３頭の敵を相手にするから「勝ったり負けたり」するのであって、２頭を相手にすると考えれば「勝ち」を確実にできるというわけです。

 

これと同じ戦略は、私自身が、司法試験の受験中、短答式試験のときに使っていました。私の立てた作戦はこうです。

 

当時の司法試験の短答式試験（択一試験）は、憲法・民法・刑法の各２０問、合計６０問を３時間で解くというものでした。これだと、平均１問を３分で解くという計算です。しかし、これは私にとっては、少々きついものでした。いつも時間不足になり、ケアレスミスのチェックもする時間がない、という感じでした。択一試験には、得意な人もいて、そういう人はいつも時間を余らせていましたが、私には、到底無理でした。一問一問を短い時間で解けるようになればよいのですが、もともと文章を読むのがそれほど速くもなく、理解にも時間がかかるので、そういうわけにもいきません。無理に時間を短くしようとすると、解き方がザツになり、ミスが出てしまうのでした。

 

そこで、私が考えたのが、この孫子の使った作戦でした。

 

当時の短答式試験の合格点は、毎年一定というわけではなかったのですが、大体４１点から４５点くらいで、４５点を超えることはありませんでした（その後、私が合格した後は４８点の年などもありましたが）。そこで、私が当時考えたのは、４５問だけ十分に時間をかけて解き、全問正解する。そのために、憲法・民法・刑法で各５問ずつを「捨てる」ということでした。

 

ただし、この「捨てる問題」は、時間をかけてもどうせ解けない問題を捨てる、ということであって、機械的に捨てるわけではありません。とにかく、４５問だけは確実に全問正解できなければならないわけですから、「捨てる１５問」は、難しい問題上位１５問を捨てる必要があるわけです。そのため、問題に着手してから３０秒以内に、その問題が「解けそうもないかどうか」を判断し、「解けない」と見切った場合は、思い切って即座にその問題を捨てて、次の問題に移る、というやり方をします。

 

この３０秒以内の「見切り」と、迷わず捨てる「思い切り」が、この作戦のポイントです。そして、最後まで解いてみて、結果的に１５問以上捨ててしまった場合は、その中で一番解けそうな問題から再度順に解いていきます。

 

この作戦は、本当に効果的でした。このような作戦をとるようになってから、私自身、短答式試験には、まったく困らなり、むしろ得点は従来よりも上がったのでした。

 

捨てるのがイヤなら優先順位でもよい　（2.2.2）

 

しかしそうは言っても、実際には、勉強すべき範囲をバッサリと削るのは、なかなかに勇気の要るものです。

 

どうも「捨てる」ということに、人は抵抗感を感じるのだと思います。事実、私の部屋などは、捨てられないガラクタばかりで溢れています。それはともかく、「敵を小さくする」という戦略としては、「捨てる」ほかに、「優先順位をつける」ということでも間に合います。

 

例えば、試験勉強の例で言えば、最初によく考えて、最優先で自分のやるべき勉強の範囲を決めます。そして、次に、もし時間に余裕があったならばやるべき次の範囲を決めることにします。そしてさらに、それでも時間が余ったらやるべき範囲を決めます。こんな感じに優先順位を付け、第１順位が終わらなかったら、第２順位には手を着けない、第２順位が終わらなかったら第３順位には手を着けない、と決めます。

 

まあ、当然な話ですよね。もっとも大事なことが終わっていないのに、それよりも重要度の低いものに手を出すというのは、どうかしています。そして、このように考えるならば、捨てたり、削ったり、というのとは異なり、割と気楽に範囲の限定ができると思います。どうせ、第１順位が終われば、第２順位に手を着けることができるからです。
そこで、このような考えに基づき「第１順位」の範囲を、本当に最重要な範囲に限定するといいでしょう。

 

先ほど出した、私の短答式試験対策の作戦ですが、これも実際には「捨てる」というよりは、解くべき優先順位を付けていると言えます。事実、全問正解すべき４５問をすべて解き切って時間が余れば、もちろん１５問の中から簡単そうなものから解いてみるわけですから。しかし、その１５問は、そもそも解けそうもないと考えてとりあえず捨てた問題ですし、すでにノルマの４５問は解いてしまっているので、気が楽です。もし１問でも、２問でも解ければ、万一、４５問の中に不正解があったとしても、救われると考えることができます。ま、保険をかけ、合格を確実にするためのものです。そして、そんな気楽な気分で解くと、これがまた、解けそうもないと思っていた問題がふと解けたりするから、人間とは不思議なものです。

 

それはともかく、まず、自分がやらなければならないことに優先順位をつけ、これが終わらない限りは次へ手を出さない、と自分を戒めることにより「手を広げすぎて、どれもこれもが中途半端になってしまい、結果、総崩れ」という最悪の事態は避けることができます。

≪前の記事へ　　　次の記事へ≫